Multiple Rotated Surfaces

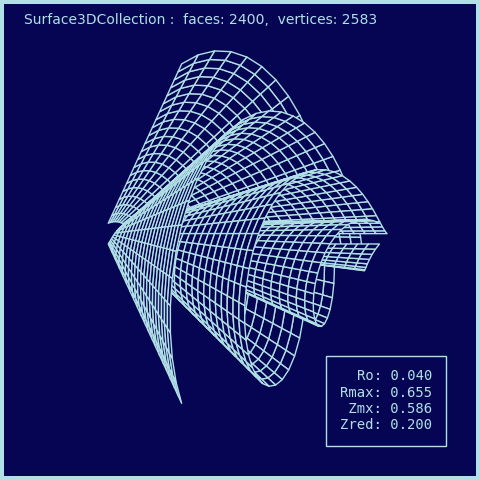
The function was developed from the geometry desscribed in the Archimedes Spiral Wind Turbine reference. An animation of the above geometry is shown in the Wind Turbine example.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

#.. Spiral wind turbine

# 1. Define function to examine .....................................
color,ecolor = [0.02,0.02,0.33],'powderblue'
Ro,Rmax,Zmx,Zred = 0.04, .655, 0.586, 0.2

def blade( position=None ) :
    def blade_geom(rtz) :
        r,t,z = rtz       #  0 < t < 2pi  and  -1 < z < 1
        Znorm = (z+1)/2   #  normalized coor: 0 < Znorm < 1
        dltR = (Rmax - Ro)/(2*np.pi)
        Ra = dltR*(t + (Ro/dltR)  )
        R = Ro + (Ra-Ro)*Znorm
        G = Zred*( 1 - t/(2*np.pi) )
        F = 1 -Zmx*t/(2*np.pi)
        Z = (F-G)*Znorm + G
        return 2*R, t, 2*Z-1
    bladeN = s3d.CylindricalSurface.grid(20,40, 'x', color=color)
    bladeN.map_geom_from_op(blade_geom)
    if position is not None:
        bladeN.transform(s3d.eulerRot(position,0))
    return bladeN

# 2. Setup surfaces .................................................

surface = blade() + blade(120) + blade(-120)
surface.transform( s3d.eulerRot(0,90)  )
surface.set_edgecolor(ecolor)

# 3. Construct figure, add surface, plot ............................
minmax = (-.9,.9)
param = 'Ro: {:.3f}\nRmax: {:.3f}\n Zmx: {:.3f}\nZred: {:.3f}'.format(Ro,Rmax,Zmx,Zred)
fig = plt.figure(figsize=plt.figaspect(1),constrained_layout=True,facecolor=ecolor)
fig.text(0.05,0.95,str(surface), ha='left', fontsize='medium', color=ecolor)
fig.text(0.90,0.10,param,ha='right', va='bottom', fontsize='medium', color=ecolor, 
    fontfamily='monospace', bbox={'edgecolor': ecolor, 'facecolor': color, 'pad': 10} )
ax = plt.axes(projection='3d', aspect='equal', proj_type='ortho',facecolor=color)
ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
ax.set_axis_off()
ax.view_init(0,-155)

ax.add_collection3d(surface)

plt.show()