World, Hello

Implicit functions, which are used to construct surfaces, take the form:

f(x,y,z) = 0

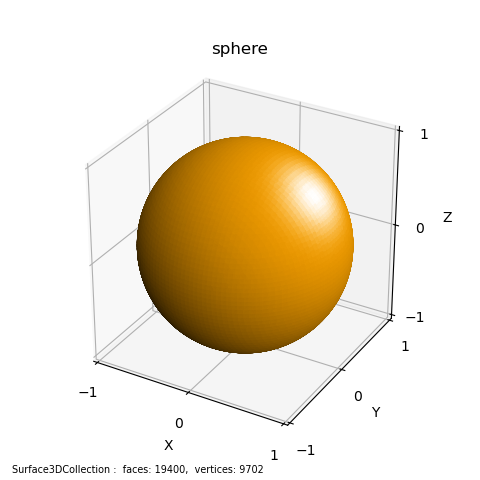
For the simple case of a sphere of unit radius:

f(x,y,z) = x² + y² + z² - 1

which is the sphere function in the code, below. This function is the first argument to the implsurf method.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

#.. World Hello

def sphere(xyz):
    x,y,z = xyz
    f = x**2 + y**2 + z**2 - 1.0
    return f

rez,dmn = 5, 1.1
surface = s3d.Surface3DCollection.implsurf( sphere,rez,dmn,color='orange')

#.................................................................
fig = plt.figure(figsize=plt.figaspect(1))
mnmx = (-1,0,1)
fig.text(0.025,0.01,str(surface), ha='left', va='bottom', fontsize='x-small')
ax = plt.axes(projection='3d', aspect='equal')
ax.set_title(surface.name)
ax.set(xlabel='X',ylabel='Y',zlabel='Z',xticks=mnmx,yticks=mnmx,zticks=mnmx)
ax.add_collection3d(surface.shade().hilite(focus=2))

fig.tight_layout(pad=3)
plt.show()

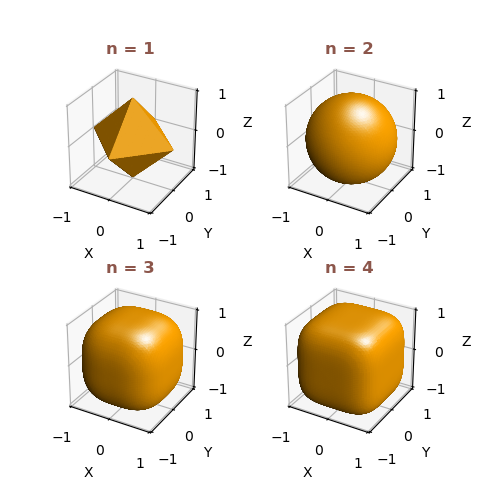
The following example shows multiple calls to a function to compare the effect of the coeficient, n.

f_n(x,y,z) = |x|ⁿ + |y|ⁿ + |z|ⁿ - 1

The function is called a Supersphere , referenced from Wolfram Mathworld.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

#.. Supersphere

def superSphere(xyz,N):
    x,y,z = xyz
    f = np.abs(x)**N + np.abs(y)**N +np.abs(z)**N - 1.0
    return f

fig = plt.figure(figsize=plt.figaspect(1))
rez,dmn,mnmx = 5,1.1,(-1,0,1)
for i in range(1,5) :
    ax = fig.add_subplot(220+i, projection='3d', aspect='equal')
    ax.set_title('n = '+str(i),fontweight='bold',color='tab:brown')
    ax.set(xlabel='X',ylabel='Y',zlabel='Z',xticks=mnmx,yticks=mnmx,zticks=mnmx)
    sphere = lambda xyz : superSphere(xyz,i )
    surface = s3d.Surface3DCollection.implsurf( sphere,rez,dmn,color='orange')
    ax.add_collection3d(surface.shade().hilite(.95,direction=[1,-0.7,2],focus=2))

fig.tight_layout(pad=3)
plt.show()