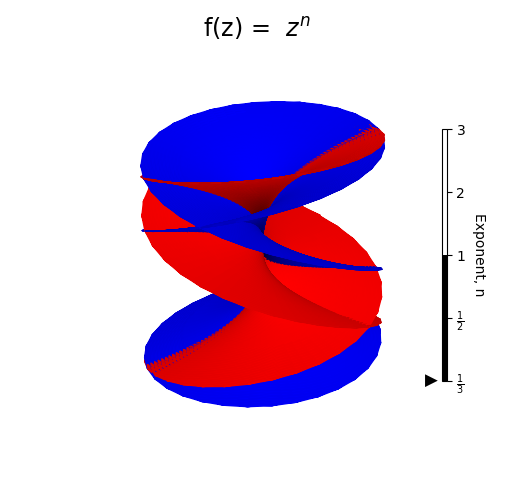
Complex Number to a Power

Animation control:

Visualization	Frame Value
Surface geometry	functional parameter per frame
Surface position	fixed to the coordinate axis
Surface color	color per frame
Shading and highlighting	fixed to the coordinate axis
Axis coordinate	constant

Based on the static plots from the Parametric Set example.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import s3dlib.surface as s3d
import s3dlib.cmap_utilities as cmu

# 0. Define animation control parameters ............................

totalTime, f_domain, numFrames = 14, (0.0,1.0), 120   # time in seconds
frames=np.linspace(*f_domain, numFrames, endpoint=False)
interval = int(1000.0*totalTime/numFrames)          # milliseconds

# 1. Define functions to examine ....................................

real = True
imaginary =  not real

def pover_Z(rtz, isReal, N) :
    r,t,z = rtz
    A = np.power(r,N)
    alpha = N*t if N>1 else t
    if isReal : Z = A*np.cos(alpha)
    else :      Z = A*np.sin(alpha)
    return r,alpha/N,Z

elev,azim,lightDir = 20, -150, [1,0,1]

xpont = [0.333, 0.5,  1,   2,    3]                         # exponents, n
ticPs = [0,     0.25, 0.5, 0.75, 1]                         # colorbar tick positions
ticLb = [r'$\frac{1}{3}$', r'$\frac{1}{2}$', '1', '2', '3'] # colorbar labels

val =           lambda b : s3d.frame_to_value(b,xpont)[0]   # linear segment path
frame_to_beta = lambda f : 2*f if f<0.5 else 2*(1-f)        # forward to reverse sequence

def indicator_by_A(fig, A, vOld=None) :
    # 0 < A < 1
    symbol, blank = r'$\blacktriangleright$', r'$\blacksquare$'
    horz, vCen, vRng = 0.825, 0.467, 0.26
    vert = vCen + vRng*(2*A-1)
    if vOld is not None: 
        fig.text(horz,vOld,blank, ha='right', va='center', fontsize='x-large', color='w')
    fig.text(horz,vert,symbol, ha='right', va='center', fontsize='large')
    return vert

# 2. Setup and map surfaces .........................................
frame = 0.0
beta = frame_to_beta(frame)
V = val(beta)

rez=5
zMap = cmu.hsv_cmap_gradient( [.5,1,1], [1.5,1,1] )

surface = s3d.PolarSurface(rez, 'squ_c', cmap=zMap)
surface.map_cmap_from_op( lambda rtz : pover_Z(rtz,imaginary,V)[2] )
surface.map_geom_from_op( lambda rtz : pover_Z(rtz,real,V) )

# 3. Construct figure, add surfaces, and plot .....................

rtv = s3d.rtv(lightDir,elev,azim)
minmax = (-1,1) 
sm = plt.cm.ScalarMappable(cmap=cmu.binary_cmap('k','w'))
sm.set_array([])

fig = plt.figure(figsize=plt.figaspect(0.9))
ax = plt.axes(projection='3d', aspect='equal')
ax.set_title( r'f(z) =  $z^n$', fontsize='xx-large' )
ax.view_init(elev,azim)
ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
cbar = plt.colorbar(sm, ax=ax,  shrink=0.6, pad=-.05, aspect=50, ticks=ticPs )
cbar.set_label('Exponent, n', rotation=270, labelpad = 15)
cbar.ax.set_yticklabels(ticLb)
ax.set_axis_off()

ax.add_collection3d(surface.shade(0,rtv))
prevIndicator = indicator_by_A(fig, beta)

fig.tight_layout()
#plt.show()

# 4. Animation ======================================================

def update_fig(frame):
    global surface
    global prevIndicator
    surface.remove()

    beta = frame_to_beta(frame)
    V = val(beta)

    surface = s3d.PolarSurface(rez, 'squ_c', cmap=zMap)
    surface.map_cmap_from_op( lambda rtz : pover_Z(rtz,imaginary,V)[2] )
    surface.map_geom_from_op( lambda rtz : pover_Z(rtz,real,V) )
    surface.shade(0,rtv)
    prevIndicator = indicator_by_A(fig, beta, prevIndicator)

    ax.add_collection3d(surface)
    return

anim = FuncAnimation(fig, update_fig, frames, interval=interval, repeat=True)
anim.save('complex.html',writer='html')

msg = "saved {} frames, values: [{:.3f} to {:.3f}] @ {} milliseconds/frane"
print(msg.format(numFrames,np.min(frames),np.max(frames),interval))

In the above animation, the real and imaginary components are respresented by geometry and color, respectively. Changeing the highlighted lines in the above script by:

surface_I = s3d.PolarSurface(5,'hex_c', facecolor='red')
surface_I.map_geom_from_op( lambda rtz : pover_Z(rtz,imaginary,V) )
surface_R = s3d.PolarSurface(5,'hex_c', facecolor='blue')
surface_R.map_geom_from_op( lambda rtz : pover_Z(rtz,real,V) )
surface = surface_I + surface_R

both real and imaginary componets are represented as blue and red surfaces, as shown below: