Parametric Set

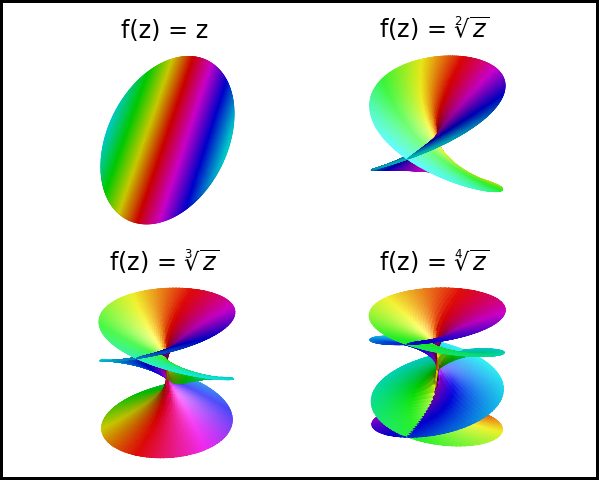
This example uses a parameterized version of the function in the Complex Number Representation, Geometry and Colormap example. An animation using a parametric variable is given in Complex Number to a Power.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d
import s3dlib.cmap_utilities as cmu

#.. Parametric Set

# 1. Define functions to examine ....................................
real = True
imaginary =  not real

def root_Z(rtz, isReal, invRoot) :
    r,t,z = rtz
    root=1/invRoot
    T=t/root
    if isReal :  Z = np.power(r,root)*np.cos(T*root)
    else :       Z = np.power(r,root)*np.sin(T*root)
    return r,T,Z

# 2 & 3. Setup surfaces and plot ....................................
rez = 6
zMap = cmu.hsv_cmap_gradient( 'cyan' , '+cyan' )
illum = s3d.rtv([1,1,1],20,205)
title = [ "" , "z" , r'$\sqrt[2]{z}$', r'$\sqrt[3]{z}$', r'$\sqrt[4]{z}$' ]

fig = plt.figure(figsize=plt.figaspect(0.8),linewidth=3,edgecolor='k')
for i in range(1,5) :
    ax = fig.add_subplot(2,2,i, projection='3d', aspect='equal')
    ax.set(xlim=(-0.8,0.8), ylim=(-0.8,0.8), zlim=(-0.8,0.8) )
    surface = s3d.PolarSurface(rez, cmap=zMap)
    surface.map_cmap_from_op( lambda rtz : root_Z(rtz,imaginary,i)[2] )
    surface.map_geom_from_op( lambda rtz : root_Z(rtz,real,i) )
    ax.set_title('f(z) = '+title[i],  fontsize='xx-large')
    surface.shade( direction=illum ).hilite(0.5,direction=illum)
    ax.add_collection3d(surface)
    ax.set_axis_off()
    ax.view_init(20, 205)

fig.tight_layout()
plt.show()