Inner Platonic Solids

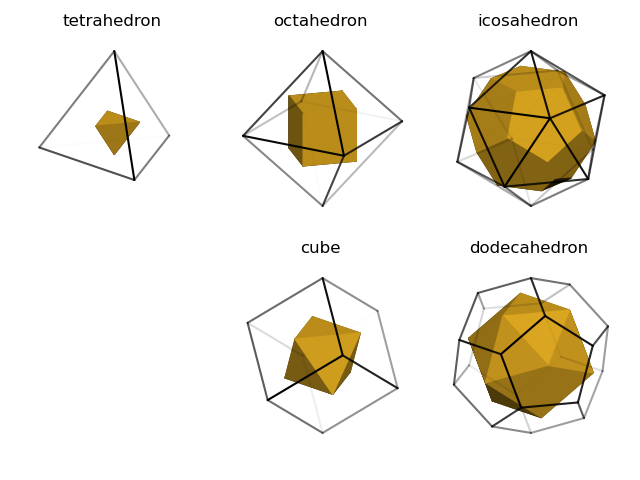
A set of vertex points which define a convex solid can be directly used to create a convex surface object using the chull method. This example uses the face centers of the platonic solids as vertex points to construct a convex hull, which itself is a platonic solid.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

#.. Inner Platonic Solid Surfaces

# 1. Define functions to examine ....................................

# 2. Setup and map surfaces .........................................
rez=4

surfaceType = ['tetra','octa','icosa','','cube','dodeca']

# 3. Construct figure, add surfaces, and plot ......................

fig = plt.figure()
minmax = (-.67,.67)
for i,stgID in enumerate(surfaceType) :   
    ax =  fig.add_subplot(231+i, projection='3d', aspect='equal')
    ax.set(xlim=(-1, 1), ylim=(-1, 1), zlim=(-1, 1))
    ax.set_axis_off()
    ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
    ax.set_proj_type('ortho')
    ax.view_init(20,-15)
    if len(stgID) == 0 : continue
    surface = s3d.SphericalSurface.platonic(0,stgID)
    edges = surface.edges
    edges.set_color('k')
    centers = np.array(surface.facecenters).T
    ax.set_title(surface.name, fontsize='large')
    innerSurface = s3d.Surface3DCollection.chull(centers,color='goldenrod')

    ax.add_collection3d(edges.fade(0.01,0,ax=ax))
    ax.add_collection3d(innerSurface.shade())

fig.tight_layout()
plt.show()