Soccer Ball

A set of vertex points which define a convex solid can be directly used to create a convex surface object using the chull method, for example from any Johnson solid , Archimedean solid , or Platonic solid , vertices. This example uses truncated icosahedron vertices .

In other examples, such as Base Class Surface 2, Truncated Octahedron Edges, or Base Class Geometric Mapping, the face vertex indices where used to set the surface faces. Using the chull method, shown in the highlighted method, only the vertex coordinates are needed since these face indices are computed to generate the set of triangular faces. However, since input face indices are not used, the surface.intedges property is not available to indicate the edges of the pentagonal and hexagonal faces, as was used in the Truncated Octahedron Edges and Edge to Edge Surface 2 examples.

The radial distance of face centers may depend on the triangulation, as is shown in the Base Face Variations example. Using the triangular face radial distance, faces can be associated with a pentagonal or hexagonal face. In the following figure, red and blue triangles are in the hexagonal face where the green and yellow faces are in the pentagonal faces. Using this association, the triangleColor method is applied to color the pentagonal and hexagonal faces

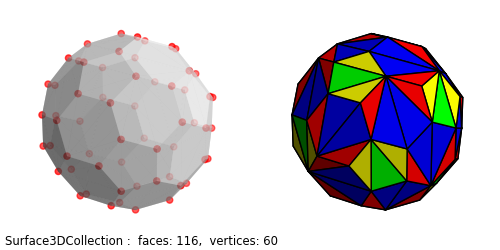
For a truncated icosahedron, there are 12 pentagons and 20 hexagons for a total of 32 faces. Since the surface object is composed of triangles, 3 for each pentagon and 4 for each hexagon, the surface object has 116 faces ( 12*3 + 20*4 = 116 ).

Once the surface is constructed, the faces are further subdivided using the triangulate method. Further geometric mapping to a constant radius produces a spherical-like surface, similar to the method in the Face Color Array example. Also note that the native coordinates for this object class is Cartesian. Consequentially, coordinate transforms (coor_convert) are used to determine the radius for these methods.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d
import s3dlib.cmap_utilities as cmu  

#.. truncated icosahedron

# 1. Define functions to examine ....................................

def generateData() :
    def permutate(A) :
        At = np.array(A).T
        Ax = At.flatten()
        Ay = At[[1,2,0]].flatten()
        Az = At[[2,0,1]].flatten()
        return np.array([Ax,Ay,Az]).T       
    phi = (1.0+np.sqrt(5.0))/2.0
    pm = [ 1.0, -1.0]
    # https://en.wikipedia.org/wiki/Truncated_icosahedron#Cartesian_coordinates
    A = [ [ 0,      y*1.0,     z*3*phi ]     for y in pm for z in pm ]
    B = [ [ x*1,    y*(2+phi), z*2*phi ]     for x in pm for y in pm for z in pm  ]
    C = [ [ x*phi,  y*2,       z*(2*phi+1) ] for x in pm for y in pm for z in pm  ]
    A = permutate(A)
    B = permutate(B)
    C = permutate(C)
    return np.concatenate( (A,B,C),axis=0)

def triangleColor(xyz) :
    r,t,z = s3d.SphericalSurface.coor_convert(xyz)
    L=len(r)
    bndA, bndB, bndC = 4.62, 4.69, 4.735
    dcolor = np.array( [[0.2]*L]*3)
    lcolor = np.array( [[0.9]*L]*3)
    color = np.where( r>bndA , dcolor,lcolor)
    color = np.where( r>bndB , lcolor, color)
    color = np.where( r>bndC , dcolor, color)
    return color

def unit_radius(xyz) :
    r,t,p = s3d.SphericalSurface.coor_convert(xyz,False)
    r = np.ones_like(r)
    return s3d.SphericalSurface.coor_convert([r,t,p],True)

# 2. Setup and map surfaces .........................................
data = generateData()

surface = s3d.Surface3DCollection.chull(data,name='soccer ball')
surface.map_color_from_op(triangleColor).triangulate(5)
surface.map_geom_from_op(unit_radius)

# 3. Construct figure, add surfaces, and plot .....................
minmax=(-.8,.8)
fig = plt.figure(figsize=plt.figaspect(1))
fig.text(0.01,0.01,str(surface), ha='left', va='bottom',
    fontsize='smaller', multialignment='left')
ax = plt.axes(projection='3d', aspect='equal')
ax.set_title(surface.name)
ax.set_axis_off()
ax.set(xlim=minmax, ylim=minmax, zlim=minmax )

ax.add_collection3d(surface.shade(0.0).hilite(1,focus=2))

fig.tight_layout(pad=1)

# =================================================================
plt.show()

The method to produce the four-color polyhedron is given below.

def triangleColor(xyz) :
    r,t,z = s3d.SphericalSurface.coor_convert(xyz)
    blue = [[0,0,1]] * len(r)
    L=len(r)
    bndA, bndB, bndC = 4.62, 4.69, 4.735
    blue =   [[0]*L, [0]*L, [1]*L]
    green =  [[0]*L, [1]*L, [0]*L]
    red =    [[1]*L, [0]*L, [0]*L]
    yellow = [[1]*L, [1]*L, [0]*L]
    color = np.where( r>bndA , green, blue)
    color = np.where( r>bndB , red,   color)
    color = np.where( r>bndC , yellow,color)
    return color