Base Class Geometric Mapping

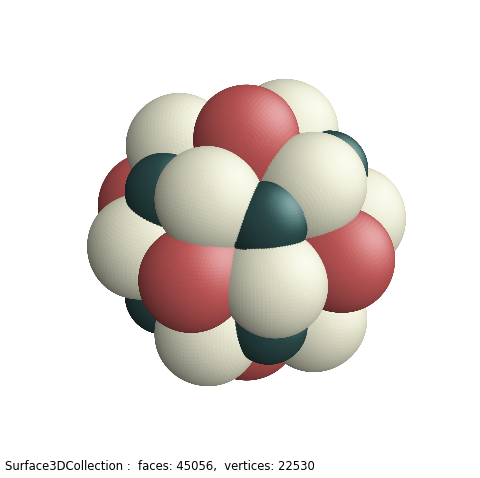
These examples use a Surface3DCollection base class, directly from vertex and face lists of the rhombicuboctahedron Archimedean solid. The base object is initially colored from the color array argument. Then the object surface is simply mapped in the radial direction after the flat surface faces are subdivided into smaller faces using the triangulate method.

The base rhombicuboctahedron is shown below. By definition, a rhombicuboctahedron has 26 faces. Since the surface object is composed of triangular faces, the 18 square faces are divided into two triangles. The surface object therefore consists of 44 triangular faces.

The geometry is mapped in the radial direction for each vertex using the method XYZtoMap. Since the coordinate system for the Surface3DCollection is the Cartesian coordinates, the radial direction is accessed using the SphericalSurface class method coor_convert. Then, the spherical coordinates are transformed back to Cartesian coordinates using the same method.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

#.. Rhombicuboctahedron Bubbles

# 1. Define Rhombicuboctahedron geometry ...........................

z = np.sqrt(2) - 1
v = [
    [ z, z, 1 ], [-z, z, 1 ], [-z,-z, 1 ], [ z,-z, 1 ],
    [ 1, z, z ], [ z, 1, z ], [-z, 1, z ], [-1, z, z ], 
    [-1,-z, z ], [-z,-1, z ], [ z,-1, z ], [ 1,-z, z ],
    [ 1, z,-z ], [ z, 1,-z ], [-z, 1,-z ], [-1, z,-z ], 
    [-1,-z,-z ], [-z,-1,-z ], [ z,-1,-z ], [ 1,-z,-z ],
    [ z, z,-1 ], [-z, z,-1 ], [-z,-z,-1 ], [ z,-z,-1 ]
]

f4 = [
    [  0, 5, 6, 1 ], [  1, 7, 8, 2 ], [  2, 9,10, 3 ], [  3,11, 4, 0 ],
    [  4,12,13, 5 ], [  6,14,15, 7 ], [  8,16,17, 9 ], [ 10,18,19,11 ],
    [ 13,20,21,14 ], [ 15,21,22,16 ], [ 17,22,23,18 ], [ 19,23,20,12 ], 

    [  0, 1, 2, 3 ],
    [  5,13,14, 6 ], [  7,15,16, 8 ], [  9,17,18,10 ], [ 11,19,12, 4 ], 
    [ 20,23,22,21 ]   
]
f3 = [
    [  0, 4, 5 ], [  1, 6, 7 ], [  2, 8, 9 ], [  3,10,11 ],
    [  20,13,12], [ 21,15,14 ], [ 22,17,16 ], [23, 19,18 ]
]

f = f4 + f3
colors = ['beige']*12 + ['indianred']*6 + ['darkslategrey']*8

def XYZtoMap(xyz) :
    r,t,p = s3d.SphericalSurface.coor_convert(xyz,False)
    r = np.ones(len(r))-0.33*r**4
    return s3d.SphericalSurface.coor_convert([r,t,p],True)

# Figure 1 =========================================================
rez = 5

surface = s3d.Surface3DCollection(v, f, name='',color=colors)
surface.triangulate(rez).map_geom_from_op(XYZtoMap)

fig = plt.figure(figsize=plt.figaspect(1))
fig.text(0.01,0.01,str(surface), ha='left', va='bottom',
    fontsize='smaller', multialignment='left')
ax = plt.axes(projection='3d', aspect='equal')
w = 0.8*surface.bounds['rorg'][1]
minmax = (-w,w)
ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
ax.set_axis_off()
ax.set_proj_type('ortho')

ax.add_collection3d(surface.shade(0.25).hilite(.5))

fig.tight_layout(pad=0)

# Figure 2 =========================================================

surface = s3d.Surface3DCollection(v, f, name='rhombicuboctahedron', color=colors)

fig = plt.figure(figsize=plt.figaspect(1))
fig.text(0.01,0.01,str(surface), ha='left', va='bottom',
    fontsize='smaller', multialignment='left')
ax = plt.axes(projection='3d', aspect='equal')
ax.set_title('\n'+surface.name)
w = 0.8*surface.bounds['rorg'][1]
minmax = (-w,w)
ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
ax.set_axis_off()
ax.set_proj_type('ortho')

ax.add_collection3d(surface.shade(0.25))

fig.tight_layout(pad=0)

# =================================================================
plt.show()