Base Face Variations

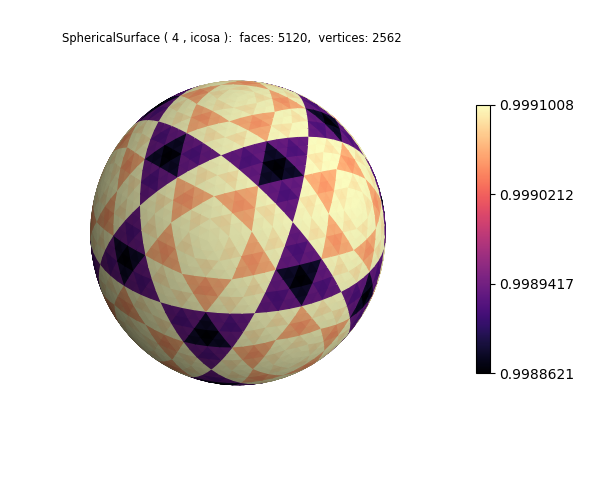
Although all surface vertices are the same length (r=1), the face centers are slightly different due to the recursive triangulation. This results in a pattern developing when the color map is based on the normalized face center radial position. As seen from the colorbar, variations in face radial position are less than 0.0035. The pattern persists for higher rez values.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

#.. Base Face Variations

# 2. Setup and map surface .........................................
rez = 4

surface = s3d.SphericalSurface(rez)
surface.map_cmap_from_op( cmap='magma' )

# 3. Construct figure, add surface plot ............................

fig = plt.figure(figsize=plt.figaspect(0.8))
ax = plt.axes(projection='3d', aspect='equal')
minmax = (-0.8,0.8)
ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
minc, maxc = surface.bounds['vlim']
plt.colorbar(surface.cBar_ScalarMappable, ax=ax, ticks=np.linspace(minc,maxc,4), shrink=0.6 )
ax.set_axis_off()
ax.set_title(str(surface),fontsize='small')

ax.add_collection3d(surface.shade(.2))

plt.tight_layout()
plt.show()

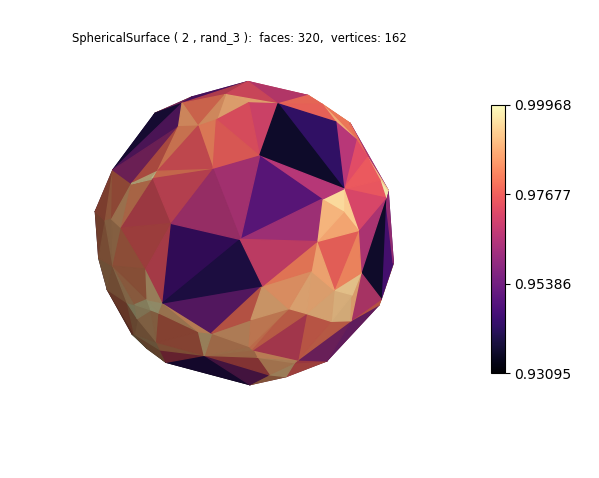
Base spherical surfaces with random triangular faces are generated using the rand class method. Replacing the surface construction by:

surface = s3d.SphericalSurface.rand(2,3)

produces the following figure. The larger the face triangles, the closer the face center is to the origin (the smaller radial distance).