Rhombicuboctahedron

The Base Class Geometric Mapping example surface.

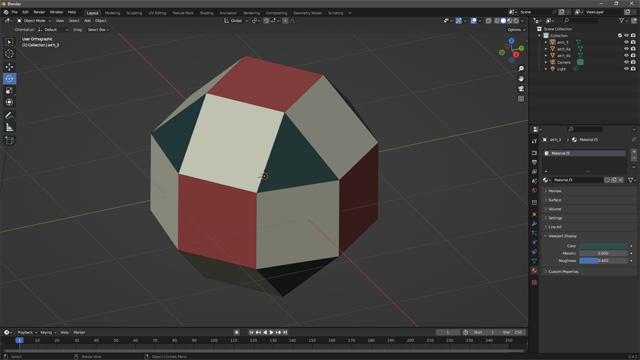
Instead of constructing a single multi-faced object as in the example, three objects are constructed based on the intended coloration. Once imported, Blender is used to individually color the three objects.

import numpy as np
import s3dlib.surface as s3d

#.. Rhombicuboctahedron

# 1. Define Rhombicuboctahedron geometry ...........................

z = np.sqrt(2) - 1
v = [
    [ z, z, 1 ], [-z, z, 1 ], [-z,-z, 1 ], [ z,-z, 1 ],
    [ 1, z, z ], [ z, 1, z ], [-z, 1, z ], [-1, z, z ], 
    [-1,-z, z ], [-z,-1, z ], [ z,-1, z ], [ 1,-z, z ],
    [ 1, z,-z ], [ z, 1,-z ], [-z, 1,-z ], [-1, z,-z ], 
    [-1,-z,-z ], [-z,-1,-z ], [ z,-1,-z ], [ 1,-z,-z ],
    [ z, z,-1 ], [-z, z,-1 ], [-z,-z,-1 ], [ z,-z,-1 ]
]

f4_A = [
    [  0, 5, 6, 1 ], [  1, 7, 8, 2 ], [  2, 9,10, 3 ], [  3,11, 4, 0 ],
    [  4,12,13, 5 ], [  6,14,15, 7 ], [  8,16,17, 9 ], [ 10,18,19,11 ],
    [ 13,20,21,14 ], [ 15,21,22,16 ], [ 17,22,23,18 ], [ 19,23,20,12 ]
] 
f4_B = [
    [  0, 1, 2, 3 ],
    [  5,13,14, 6 ], [  7,15,16, 8 ], [  9,17,18,10 ], [ 11,19,12, 4 ], 
    [ 20,23,22,21 ]   
]

f3 = [
    [  0, 4, 5 ], [  1, 6, 7 ], [  2, 8, 9 ], [  3,10,11 ],
    [  20,13,12], [ 21,15,14 ], [ 22,17,16 ], [23, 19,18 ]
]

surf_3  = s3d.Surface3DCollection(v, f3)
surf_4A = s3d.Surface3DCollection(v, f4_A)
surf_4B = s3d.Surface3DCollection(v, f4_B)

s3d.save_surfgeom_to_obj('obj_files/arch_3.obj', surf_3)
s3d.save_surfgeom_to_obj('obj_files/arch_4a.obj',surf_4A)
s3d.save_surfgeom_to_obj('obj_files/arch_4b.obj',surf_4B)