Spherical Coordinates to XYZ

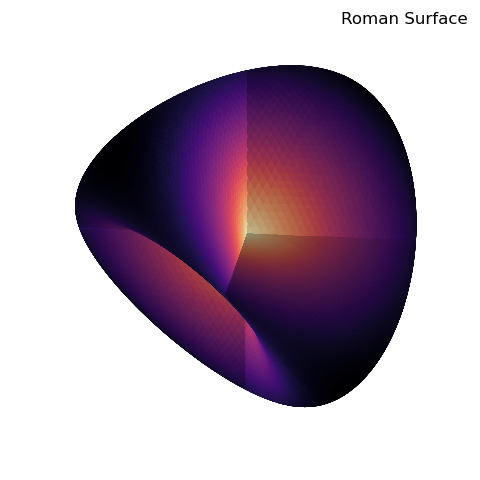
A detailed description of the Roman surface is found in Wikipedia where the functional definition is located.

import numpy as np
from matplotlib import pyplot as plt
import s3dlib.surface as s3d

#.. Spherical Coordinates to XYZ

# 1. Define function to examine ....................................

def roman(rtp) :
    r,t,p = rtp
    ct, st = np.cos(t), np.sin(t)
    cp, sp = np.cos(p), np.sin(p)
    cp_sp = cp*sp
    ct_st = ct*st
    x = cp*ct_st
    y = sp*ct_st
    z = cp_sp*np.square(ct)
    return x,y,z

# 2. Setup and map surface .........................................
rez = 6

surface = s3d.SphericalSurface(rez,basetype='octa_c',minrad=0.001)
surface.map_geom_from_op( roman, returnxyz=True )
surface.map_cmap_from_op( lambda rtp: rtp[0] , cmap='magma_r' )

# 3. Construct figure, add surface plot ............................

fig = plt.figure(figsize=plt.figaspect(1))
fig.text(0.975,0.975, "Roman Surface", ha='right', va='top', fontsize='larger', multialignment='right')
ax = plt.axes(projection='3d', aspect='equal')
minmax = (-.38,.38)
ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
ax.set_axis_off()
ax.view_init(elev=20, azim=-83)

ax.add_collection3d(surface.shade(.5))

fig.tight_layout()
plt.show()