Schwarz P Surface

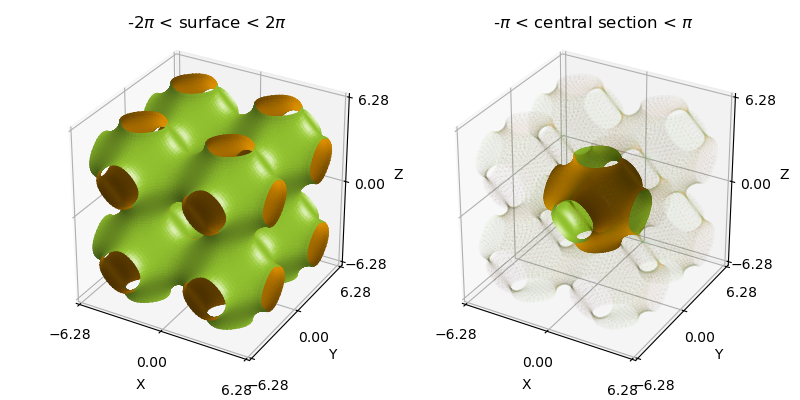
Using different colors to differentiate the front and back of a surface may clarify visualizations for non-open surfaces. The above figure uses such coloring to show that inner and outer volumes are identical with a π translation.

import copy
import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d
import s3dlib.cmap_utilities as cmu

#.. Schwarz P Surface

def schwarzP(xyz) :
    x,y,z = xyz
    return np.cos(x) + np.cos(y) + np.cos(z)

# ...................................................................
bcmap = cmu.binary_cmap('orange', 'yellowgreen')

fig = plt.figure(figsize=(8,4))
mnmx,tck = (-2*np.pi, 2*np.pi), (-2*np.pi, 0, 2*np.pi)

for i,[dmn,title] in enumerate ( [ \
        [2*np.pi, r'-2$\pi$ < surface < 2$\pi$'],
        [  np.pi,  r'-$\pi$ < central section < $\pi$']   ] ) :
    ax =fig.add_subplot(121+i, projection='3d',aspect='equal')
    ax.set(xlabel='X',ylabel='Y',zlabel='Z',title=title,
        xlim=mnmx,  ylim=mnmx,  zlim=mnmx, 
        xticks=tck, yticks=tck, zticks=tck )
    surface = s3d.Surface3DCollection.implsurf( schwarzP,6,dmn, cmap=bcmap )
    surface.map_cmap_from_normals(direction=ax)
    if i == 0 :
        fullSurf = copy.copy(surface)
        fullSurf.set_surface_alpha(0.01)
    else :
        surface = surface + fullSurf
    ax.add_collection3d(surface.shade(.3).hilite(0.7,focus=2))

fig.tight_layout(pad=2)
plt.show()