Nodal Surface

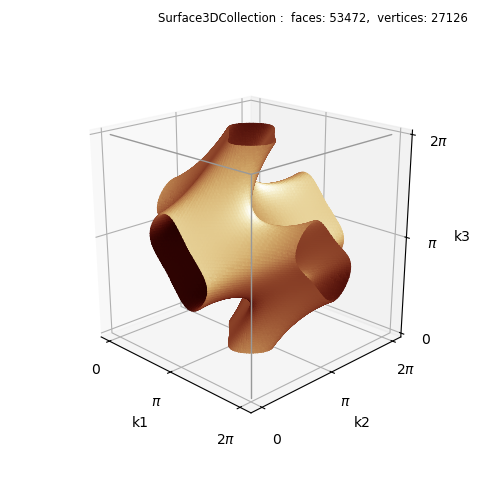
The functional expression is given in the Hyperbolic Matter article.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d
import s3dlib.cmap_utilities as cmu

# 1. Define function to examine ....................................

def nodesurf(xyz) :
    x,y,z = xyz
    i = 1j
    h = 1 + np.exp(i*x) + np.exp(i*y) + np.exp(i*z)  
    return np.abs(h)-1

# 2. Setup and map surface .........................................
pi,p2 = np.pi, 2*np.pi
cmap= cmu.rgb_cmap_gradient('red','khaki')

surface = s3d.Surface3DCollection.implsurf( nodesurf,8,[0,p2])
surface.map_cmap_from_normals(cmap )

# 3. Construct figure, add surface, and plot ......................
tks = [0,pi,p2]
tklabels =  ['0',r'$\pi$',r'2$\pi$']
fig = plt.figure(figsize=plt.figaspect(1))
fig.text(0.975,0.975,str(surface), ha='right', va='top', fontsize='smaller')
ax = plt.axes(projection='3d', focal_length=0.5, aspect='equal' )
ax.set(xlabel='k1', ylabel='k2', zlabel='k3', xticks=tks, yticks=tks, zticks=tks )
ax.view_init(20,-45)
ax.set_xticklabels(tklabels)
ax.set_yticklabels(tklabels)
ax.set_zticklabels(tklabels)
s3d.auto_scale(ax,surface)

ax.add_collection3d(surface.shade(.1).hilite())

vE,iE = [ [0,0,p2], [p2,0,p2], [p2,p2,p2], [p2,0,0] ], [ [0,1,2],[1,3]]
ax.add_collection3d( s3d.ColorLine3DCollection(vE,iE,color='0.6',lw=1) )

fig.tight_layout(pad=0)
plt.show()