Earth Klein

Image mapping is applied following surface object instantiation and followed by geometric mapping. The geometric mapping includes parametric functional mapping. This is shown for the mapping to the Klein bottle geometry.

import numpy as np
from matplotlib import pyplot as plt
import s3dlib.surface as s3d

#.. Earth image mapped to a klein bottle.

# 1. Define function to examine ....................................
def klein_bottle(rtz) :
    r,t,z = rtz
    u = np.pi*(1-z)/2
    v = -t
    cU, sU = np.cos(u), np.sin(u)
    cV, sV = np.cos(v), np.sin(v)
    x = -(2/15)*cU* \
        (  ( 3 )*cV + \
           ( -30 + 90*np.power(cU,4) - 60*np.power(cU,6) + 5*cU*cV )*sU  )
    y = -(1/15)*sU* \
        (  ( 3 - 3*np.power(cU,2) -48*np.power(cU,4) +48*np.power(cU,6) )*cV + \
           (-60 + ( 5*cU - 5*np.power(cU,3) - 80*np.power(cU,5) + 80*np.power(cU,7) )*cV  )*sU  )
    z = (2/15)*( 3 + 5*cU*sU )*sV
    return x,y,z

# 2. Setup and map surface .........................................
img_fname, rez = 'data/earth.png', 7

surface = s3d.CylindricalSurface(rez, color='w' )
surface.map_color_from_image(img_fname)
surface.map_geom_from_op( klein_bottle, returnxyz=True )
surface.transform(s3d.eulerRot(90,-90),translate=[0,0,2])

# 3. Construct figure, add surface plot ............................
minmax = (-1.5,1.5)
fig = plt.figure(figsize=plt.figaspect(1))
ax = plt.axes(projection='3d', aspect='equal')
ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
ax.set_title(surface.name)
ax.set_axis_off()
ax.view_init(elev=20, azim=-125)

ax.add_collection3d(surface.shade(.5,ax=ax).hilite(ax=ax))

fig.tight_layout()
plt.show()

Image mapping with subsequent geometric mapping can be in the various native coordinate surfaces, as shown below.

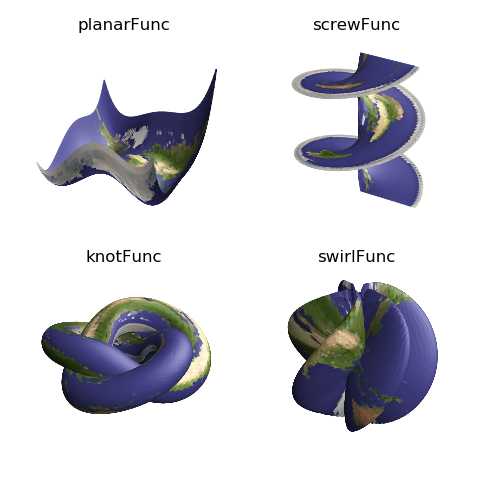
import numpy as np
from matplotlib import pyplot as plt
import s3dlib.surface as s3d

#.. Image mapping for different coordinate systems.

# 1. Define functions to examine ....................................
def planarFunc(xyz) : # Himmelblau
    x,y,z = xyz
    X,Y = 5*x, 5*y
    Z1 = np.square( X*X + Y - 11 )
    Z2 = np.square( Y*Y + X - 7  ) 
    Z = (Z1 + Z2)/500 - 1
    return x,y,Z

def screwFunc(rtz) :
    r,t,z = rtz
    T = 2*t
    Z = 0.2*(T - 2*np.pi)
    return r,T,Z

def knotFunc(rtz) :
    r,t,z = rtz
    rho,zeta,delta,scale = 0.25, 0.25, 0.3, 1.1
    R = (1-rho)*(1-delta*np.sin(3*t)) + rho*np.cos(z*np.pi) 
    Z = rho*np.sin(z*np.pi) + zeta*np.cos(3*t)
    return scale*R, 2*t, scale*Z

def swirlFunc(rtp) :
    r,t,p = rtp
    R = 0.4*(2 + np.sin(5*t + 3*p))
    return R,t,p
 
# 2. Setup and map surfaces .........................................
img_fname, rez = 'data/earth.png', 5

planar = s3d.PlanarSurface(rez,basetype='oct1')
planar.map_color_from_image(img_fname)
planar.map_geom_from_op(planarFunc)

screw = s3d.PolarSurface(rez, basetype='hex_s')
screw.map_color_from_image(img_fname)
screw.map_geom_from_op( screwFunc)

knot = s3d.CylindricalSurface(rez, basetype='squ_s')
knot.map_color_from_image(img_fname)
knot.map_geom_from_op( knotFunc ) 

swirl = s3d.SphericalSurface(rez)
swirl.map_color_from_image(img_fname)
swirl.map_geom_from_op( swirlFunc )

# 3. Construct figure, add surfaces, and plot ......................
minmax = (-.9,.9)
fig = plt.figure(figsize=plt.figaspect(1) )
for i,surface in enumerate( [planar,screw,knot,swirl] ) :
    ax = fig.add_subplot(221+i, projection='3d', aspect='equal')
    ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
    ax.set_title(surface.name)
    ax.set_axis_off()

    ax.add_collection3d(surface.shade().hilite(.5))

fig.tight_layout()
plt.show()