Volumetric Plot

This is a comparison to the 3D voxel / volumetric plot Matplotlib example.

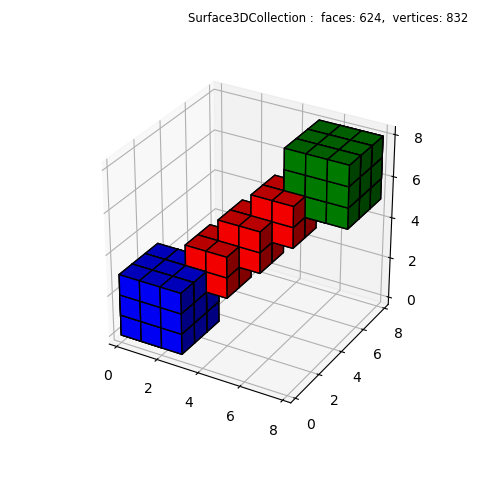
S3Dlib does not have a ‘voxel’ object. In this example, a ‘CubicSurface’ object was used to represent a voxel. The method to produce the plot is just to position the set of resized objects to corresponding coordinates. This method was also used to construct the salt unit cell example.

import numpy as np
from matplotlib import pyplot as plt
import s3dlib.surface as s3d

# +----------------------------------------------------------------------------
# |  The following code between the ========= comments was copied DIRECTLY from
# |  https://matplotlib.org/stable/gallery/mplot3d/voxels.html#sphx-glr-gallery-mplot3d-voxels-py
# +----------------------------------------------------------------------------
# ===================================================== start of copy.
# prepare some coordinates
x, y, z = np.indices((8, 8, 8))

# draw cuboids in the top left and bottom right corners, and a link between
# them
cube1 = (x < 3) & (y < 3) & (z < 3)
cube2 = (x >= 5) & (y >= 5) & (z >= 5)
link = abs(x - y) + abs(y - z) + abs(z - x) <= 2
# ===================================================== end of copy.
# 1. Define functions to examine ....................................

def cubeCenters(space) :
    x,y,z = np.shape(space)
    position = []
    for ix in range(x) :
        for iy in range(x) :
            for iz in range(x) :
                if(space[ix,iy,iz]): position.append([ix,iy,iz])
    return  np.array(position,dtype=float)

groupPos = {}
groupPos['red'] =   cubeCenters(link)
groupPos['blue'] =  cubeCenters(cube1)
groupPos['green'] = cubeCenters(cube2)

# 2. Setup and map surfaces .........................................
unitCubes = None
for cubeName, cubePos in groupPos.items() :
    for pos in cubePos :
        cube = s3d.CubicSurface(0, facecolor=cubeName)
        cube.transform(scale=0.5 , translate=pos+0.5)
        if unitCubes is None : unitCubes = cube
        else : unitCubes += cube

unitCubes.shade(direction= (0,-1,0.5) )
unitCubes.set_edgecolor('k')

# 3. Construct figure, addsurfaces, and plot ......................
minmax = (-0.2,8.2)
fig = plt.figure(figsize=plt.figaspect(1))
fig.text(0.975,0.975,str(unitCubes), ha='right', va='top', fontsize='smaller')
ax = plt.axes(projection='3d', aspect='equal')
ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
ax.add_collection3d(unitCubes)

plt.show()