Vector Fields

Vector fields in 3D can be constructed using the Vector3DCollection constructor or from four surface object methods.

Since the Vector3DCollection is derived from the Line3Dcollection, a vectorfield object is added to a 3D axis in the identical way a surface is added to the axis, e.g.:

axes.add_collection3D(vectorfield)

Vector Base Class

Creating a Vector3DCollection object from the constructor is as follows:

vf = Vector3DCollection( location, vect, alr=None, name=None )

where location and vect are the vector tail coordinate array and vect is the vector component array, respectively. Both arrays are N X 3 arrays and use xyz Cartesian coordinates. The parameter alr is the head size to vector magnitude ratio, axis length ratio, which defaults to 0.25.

A simple demonstration of creating a vector field is shown in the 3D quiver plot example.

Vectors from Surface Methods

Vector fields constructed using surface object methods are based on the coordinates of the surface object. These methods provide:

• Face normals

• Vectors at a position, ( u, v, w )

• Surface displacements, (δx, δy, δy)

• Surface to surface positional differences, (δx, δy, δy)

The methods return a vector field object of type Vector3DCollection. All methods have the named parameters:

named parameter	type	default value
scale	numeric	1
width	numeric	surface linewidth
alr	numeric	0.25
color	Matplotlib color	‘black’

The scale argument is a multiplier for the length. The width argument controls the line thickness with the default being the surface linewidth named argument of the constructor (same as the edge linewidths).

In the following discussion, the named parameters in the method description are omitted for clarity to highlight the main controlling arguments. The surface method returns a vector field object labeled vf.

Face Normals

The method is:

vf = surface.facenormals()

The length of the vectors is proportional to the average size of the triangular faces. As the surface rez increases, the length decreases. The length of the vector can also be set by assigning the ‘scale’ method argument. The vectors are centered at each triangular face, normal to the face, as illustrated below.

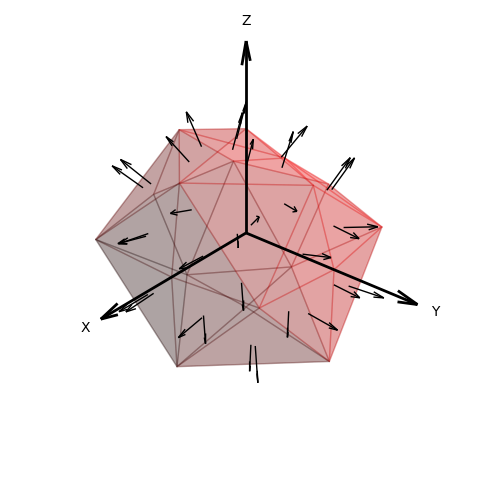
An example of this vector field is given in Face Normals Vector Field.

Vectors at a Coordinate

The method is:

vf = surface.vectorfield_from_op( op, returnxyz=False )

The op argument is a function which takes a 3 x N array argument in the native coordinate system. The function returns the 3 x N array for the vector in u,v,w coordinates, aligned using the native coordinates at each coordinate, as shown below for the cylindrical and spherical coordinates.

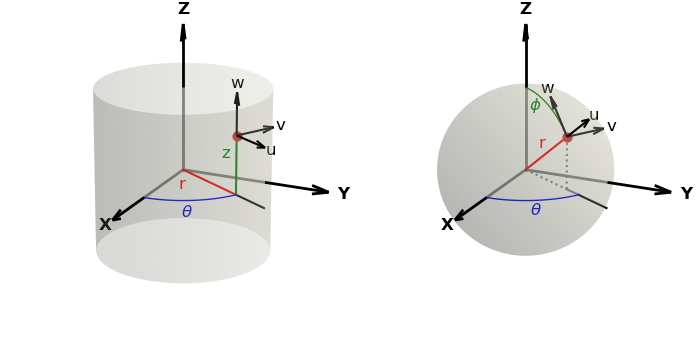
The uvw axes are aligned with the axes for the planar coordinate system. For the polar coordinates, the uvw axes are similar to the cylindrical coordinates. If the returnxyz argument is True, uvw are in planar coordinates. The vectors are located at each surface vertex, as illustrated in the figure below.

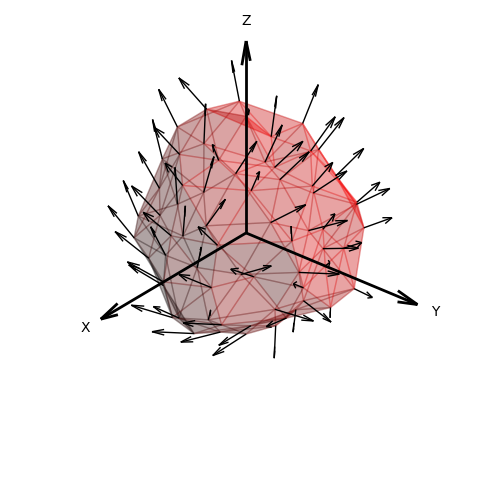
An example of this vector field is given in Vector Field in Cylindrical Coordinates.

Surface to Surface

The method is:

vf = surface.vectorfield_to_surface( surf )

The surf argument is a surface object which is the same type and rez as the calling surface object. The vector at each vertex of the surface object points to the corresponding vertex in the surf argument object, as shown below.

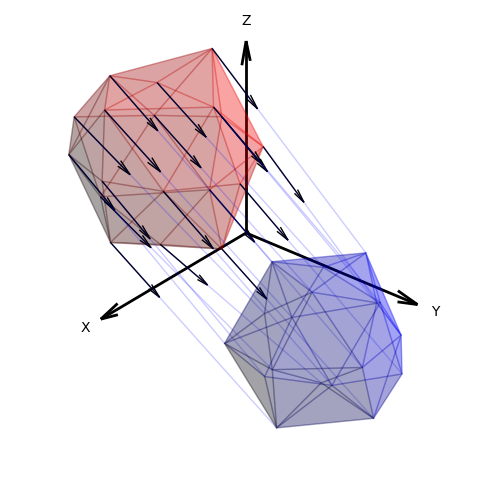
Surface Displacements

The method is:

vf = surface.dispfield_from_op( op, returnxyz=False, ussbase=False )

The op argument is a function which takes a 3 x N array argument in the native coordinate system. The function returns the 3 x N array for the vector in native coordinates. If the returnxyz argument is True, uvw are in xyz coordinates.

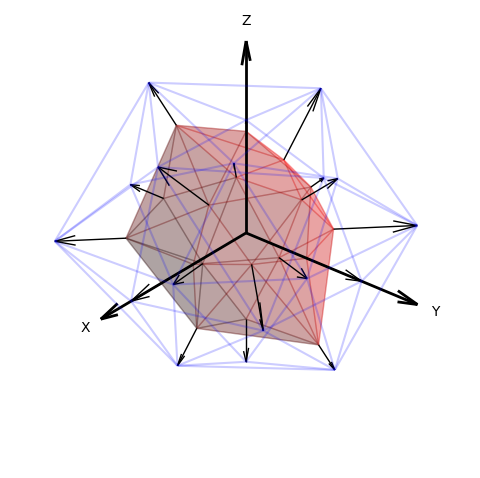
This method is similar to the geometric mapping using a function as:

surface.map_geom_from_op( op )

This difference is that instead of transforming the surface shape using the map function, vectors indicate how each surface vertex will be mapped for the function without modifying the surface geometry. This is illustrated above using the blue edges for the ‘mapped’ surface.

This function is equivalent to the vectorfield_to_surface method if a transition surface is created as:

import copy
'''
code here
'''
surf = copy.copy(surface)
surf.map_geom_from_op( op )
vf = surface.vectorfield_to_surface( surf )