Egg Shape

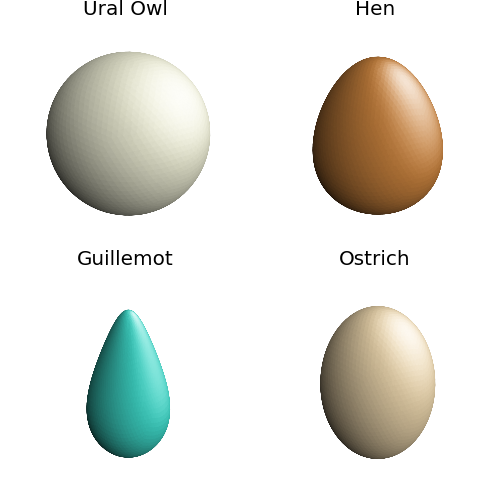
The ‘universal’ formula for egg shape are from Narushin et al , as discussed in the Christian Hill website.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

# Egg shapes

# 1. Define functions to examine ....................................

def yegg(x, L, B, w, D):
    """
    function copied directly from:
    https://scipython.com/blog/a-universal-formula-for-egg-shape/
    along with coefficients for the four eggs.
    """
    fac1 = np.sqrt(5.5*L**2 + 11*L*w + 4*w**2)
    fac2 = np.sqrt(L**2 + 2*w*L + 4*w**2)
    fac3 = np.sqrt(3)*B*L
    fac4 = L**2 + 8*w*x + 4*w**2
    return (B/2) * np.sqrt((L**2 -4*x**2) / fac4) * (
        1 - (fac1 * (fac3 - 2*D*fac2) / (fac3 * (fac1 - 2*fac2)))
     * (1 - np.sqrt(L*fac4 / (2*(L - 2*w)*x**2
                    + (L**2 + 8*L*w - 4*w**2)*x + 2*L*w**2 + L**2*w + L**3))))

def egeom( rtp, v ) :
    x,y,z = s3d.SphericalSurface.coor_convert(rtp,True)
    w = yegg(z, *v )
    R = np.sqrt(z*z + w*w)
    P = np.arccos(z/R)
    return R,rtp[1],P

# 2. Setup and map surfaces .........................................
L=1
eggs = [ [ 'Ural Owl',  'beige',     [ L,   L,   0, L*np.sqrt(3)/2] ], 
         [ 'Hen',       'peru',      [ L, 0.8, 0.1, 0.6 ] ],
         [ 'Guillemot', 'turquoise', [ L, 0.5, 0.1, 0.3 ] ],
         [ 'Ostrich',   'wheat',     [ L, 0.7,   0, 0.6 ] ]  ]

# 3. Construct figure, add surfaces, and plot ......................
rez,minmax = 4, (-.4,0.4)
fig = plt.figure(figsize=(5,5) )
for i,egg in enumerate(eggs) :
    ax = fig.add_subplot(221+i, projection='3d', aspect='equal')
    ax.set(xlim=minmax, ylim=minmax, zlim=minmax)
    ax.set_title(egg[0], fontsize='x-large')
    ax.set_axis_off()
    surface = s3d.SphericalSurface(rez,color=egg[1]).domain(L/2)
    surface.map_geom_from_op(lambda rtp: egeom(rtp,egg[2]))
    ax.add_collection3d(surface.shade().hilite(.8))

fig.tight_layout(pad=0)
plt.show()