Alternative Visualizations

The values of implicit surface functions within a domain are visualized using alternative methods for the function:

f(x,y,z) = sin( x y z ) / ( x y z )

which exhibits Argument Value Sensitivity for anomolous visualizations for various conditions.

Surface Sets

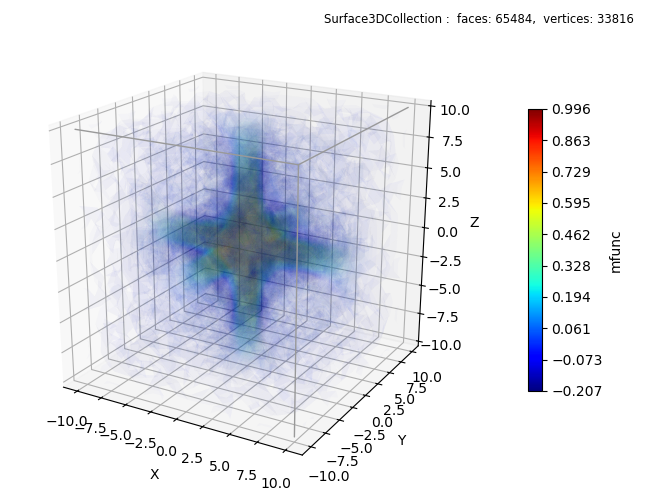
Using multiple semi-transparent contour surfaces provides a visualization of scalar values within a domain.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

# 1. Define function to examine ....................................

def mfunc(xyz) :
    x,y,z = xyz
    return np.sin(x*y*z)/(x*y*z)

# 2. Setup and map surface .........................................

surface = s3d.Surface3DCollection.implsurfSet(mfunc,1.9,10,numb=40,cmap='jet')
surface.set_surface_alpha(.015)

# 3. Construct figure, add surface, and plot ......................

fig = plt.figure(figsize=(6.5, 5))
fig.text(0.975,0.975,str(surface), ha='right', va='top', fontsize='smaller')
ax = plt.axes(projection='3d', focal_length=0.5, aspect='equal' )
ax.set(xlabel='X', ylabel='Y', zlabel='Z')
ax.view_init(20)
fig.colorbar(surface.cBar_ScalarMappable, ax=ax, pad=0.1, shrink=0.6,
    ticks=np.linspace(*surface.bounds['vlim'],10), label=surface.cname )
s3d.auto_scale(ax,surface)

ax.add_collection3d(surface.shade(.5))

vE,iE = [ [-10,-10,10], [10,-10,10], [10,10,10], [10,-10,-10] ], [ [0,1,2],[1,3]]
ax.add_collection3d( s3d.ColorLine3DCollection(vE,iE,color='0.6',lw=1) )

fig.tight_layout()
plt.show()

Value Colormapping

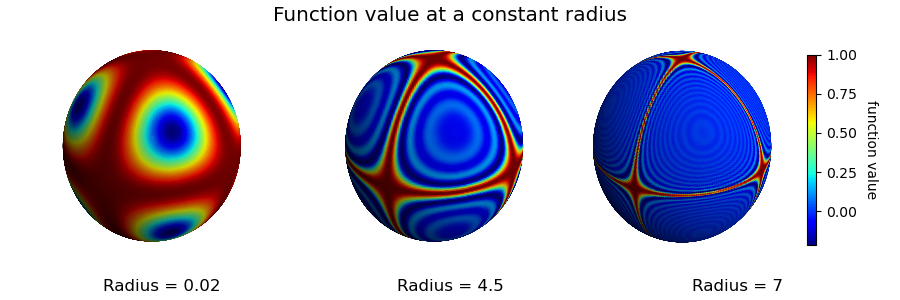
Mapping the values onto spheres illustrates large value fluctuations at larger radial distances from the origin for the cases of small functional values:

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d
import copy

# 1. Define function to examine .....................................
def mfunc(xyz) :
    x,y,z = xyz
    return np.sin(x*y*z)/(x*y*z)

val_at_R = lambda rtp : mfunc( s3d.SphericalSurface.coor_convert(rtp,True) )

# 2. Setup and map surfaces .........................................
rez,cmap = 6,'jet'
radius = [.02,4.5,7]
figTitle = 'Function value at a constant radius'
# 3. Construct figure, add surface, plot ............................
ofst = [0.18,0.5,0.82]
fig = plt.figure(figsize=(9,3))
fig.text(0.5,0.98,figTitle, ha='center', va='top', fontsize='x-large')
for i in range(3) :
    title = 'Radius = '+str(radius[i])
    ax =fig.add_subplot(131+i, projection='3d', aspect='equal')
    fig.text(ofst[i],0.02,title, ha='center', va='bottom', fontsize='large')
    ax.set_axis_off()
    surface = s3d.SphericalSurface(rez,cmap=cmap).domain(radius[i])
    surface.map_cmap_from_op( val_at_R )
    usc = .72 if i<=1 else 0.54  # compensate for colorbar space.
    s3d.auto_scale(ax,surface,uscale=1.1*usc)
    ax.add_collection3d(surface.shade())

cbar = plt.colorbar(surface.cBar_ScalarMappable, ax=ax,  shrink=0.7, pad=.1 )
cbar.set_label('function value', rotation=270, labelpad=15)

fig.tight_layout(pad=1)
plt.show()

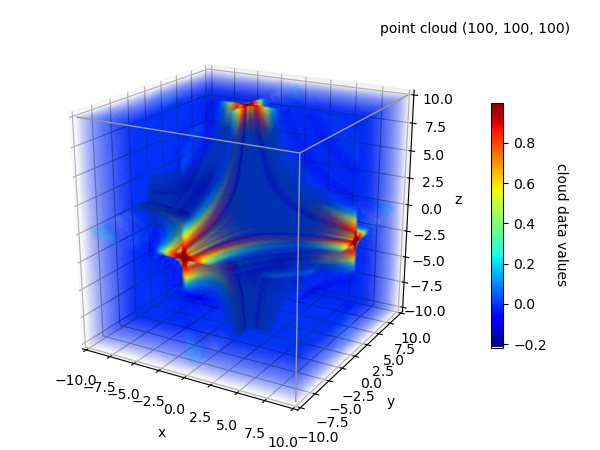
Point Cloud

An alternative to visualizing values within the domain is to plot a point cloud of values as:

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

# 1. Generate a cloud distribution to examine ............
def mfunc(xyz) :
    x,y,z = xyz
    return np.sin(x*y*z)/(x*y*z)

N,rng = 100, 10   # cloud divisions & the function domain.
cloud = mfunc( np.mgrid[ -rng:rng:N*1j,-rng:rng:N*1j,-rng:rng:N*1j ] )

# 2. Setup data ....................................................
dmn,cmap = [-10,10], 'jet'   # xyz domain to interpret the cloud
xyz, colors, scmp = s3d.get_points_from_cloud(cloud,dmn,cmap,fade=2.25)

# 3. Construct figures, add points, and plot .......................
fig = plt.figure(figsize=(6.0, 4.5))
fig.text(.95,.95,'point cloud '+str(cloud.shape),ha='right',va='top')
ax = fig.add_subplot(111, projection='3d', aspect='equal', focal_length=0.5)
ax.set(xlim=dmn,ylim=dmn,zlim=dmn,xlabel='x',ylabel='y',zlabel='z')
ax.view_init(20)

ax.scatter(*xyz, c=colors, marker='.', s=10)
cbar = plt.colorbar(scmp, ax=ax,  shrink=0.6, pad=.08 )
cbar.set_label('cloud data values', rotation=270, labelpad = 15)

vE,iE = [ [-10,-10,10], [10,-10,10], [10,10,10], [10,-10,-10] ], [ [0,1,2],[1,3]]
ax.add_collection3d( s3d.ColorLine3DCollection(vE,iE,color='0.6',lw=1) )

fig.tight_layout(pad=1.5)
plt.show()