Schwarz P Contour Surfaces within a Domain

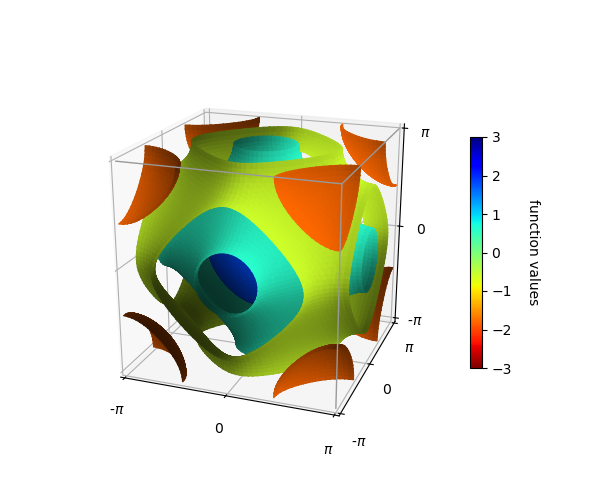
From the example Schwarz P Surface, a set of contour surfaces are generated within the domain.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

# 1. Schwarz P function to examine .................................

def schwarzP(xyz) :
    x,y,z = xyz
    return np.cos(x) + np.cos(y) + np.cos(z)

pi = np.pi
dmn,numb,cmap = [-pi,pi],4,'jet_r'

# 2. Setup and map surface .........................................

surface = s3d.Surface3DCollection.implsurfSet(schwarzP, drez=5.0, domain=dmn, numb=numb, cmap=cmap)
surface.evert()

# 3. Construct figure, add surface, and plot ......................
tks,tklabels = [-pi,0,pi], [r'-$\pi$','0',r'$\pi$']
fig = plt.figure(figsize=(6,5))
ax = plt.axes(projection='3d', aspect='equal', focal_length=0.5)
ax.set(xlim=dmn,ylim=dmn,zlim=dmn, xticks=tks, yticks=tks, zticks=tks )
ax.view_init(20,-70)
ax.set_xticklabels(tklabels)
ax.set_yticklabels(tklabels)
ax.set_zticklabels(tklabels)

cbar = plt.colorbar(surface.cBar_ScalarMappable, ax=ax,  shrink=0.6 )
cbar.set_label('function values', rotation=270, labelpad = 20)

ax.add_collection3d(surface.shade(.2) )

vE,iE = [ [-pi,-pi,pi], [pi,-pi,pi], [pi,pi,pi], [pi,-pi,-pi] ], [[0,1,2],[1,3]]
ax.add_collection3d( s3d.ColorLine3DCollection(vE,iE,color='0.6',lw=1) )

plt.show()