Domain Coloring, 2D from 3D

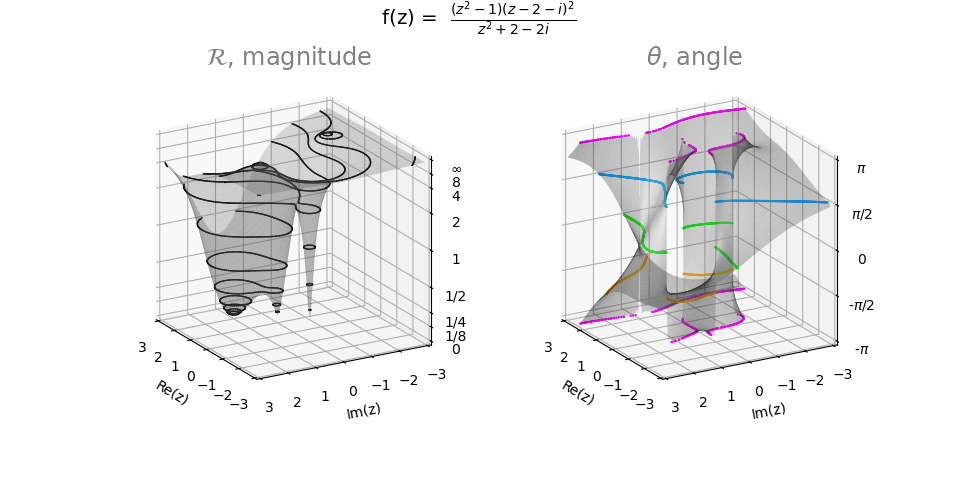
This example uses the functions from the Domain Coloring example, with the addition of a function to construct contours at the surface discontinuities.

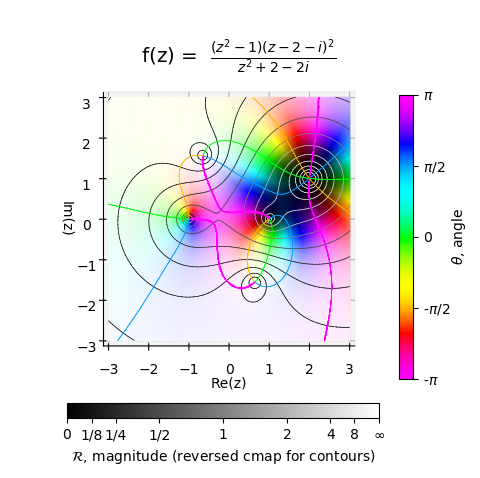
For the 2D figure below, the ‘flat’ PlanarSurface was used to construct most of the contours directly from the xy-surface. However for the discontinuous contours, the 3D θ-surface was used with the application of the discontinuity_contours function.

import numpy as np
from matplotlib import pyplot as plt
import s3dlib.surface as s3d
import s3dlib.cmap_utilities as cmu
import copy

#.. Domain Coloring 2D Contours

# 1. Define function to examine .....................................

def complexFunc(z):
    # https://en.wikipedia.org/wiki/Domain_coloring
    i = 1j
    num = (z**2 - 1)*(z - 2 -i)**2
    dem = z**2 + 2 + 2*i
    return num/dem

def funcRT(xyz) :
    x,y,z = xyz
    c = np.array(x,dtype=complex)
    c.imag = np.array(y)
    f = complexFunc(c)
    r = np.abs(f)                      #.. [0,inf]
    Z = 2*np.arctan(r)/np.pi           #.. [0,1]
    theta = (1 + np.angle(f)/np.pi)/2  #.. [0,1]
    return Z,theta 

coor_radius  = lambda c: [c[0],c[1],funcRT(c)[0]]
coor_theta   = lambda c: [c[0],c[1],funcRT(c)[1]]
isContinuous = lambda c,N: np.abs(N.T[2]) > 0.02

def domainColor(xyz) :
    Z,theta = funcRT(xyz)
    h,s,v = hsl_to_hsv(theta,1,Z)
    H = (h+5/6)%1  # cmap starts at magenta(5/6), not red(0)
    return H,s,v

def hsl_to_hsv(h, s, l):
    # from: https://gist.github.com/mathebox/e0805f72e7db3269ec22
    # Modified for arrays, used Numpy instead of python math.
    v = (2*l + s*(1-np.abs(2*l-1)))/2
    s = 2*(v-l)/v
    return h, s, v

def discontinuity_contours(surface) :
    # --- discontinuity @ theta = -pi and pi
    tnorms = surface.facenormals(v3d=False)
    tcentr = surface.facecenters
    discon = np.logical_not(isContinuous(tcentr,tnorms)) # keep discontinuous faces
    disCen = tcentr.T[discon,:]    # facecenters only facesnormals not in xy plane.
    disCen[:,2] = np.zeros(disCen.shape[0])   # flatten to xy plane @ 0 ( -pi )
    topCen = copy.copy(disCen)
    topCen[:,2] = np.ones(topCen.shape[0])    # flatten to xy plane @ 1 ( pi )
    disCen = np.concatenate((disCen,topCen),axis=0)    
    disLine = s3d.SegmentLine(disCen)
    segLens = np.linalg.norm(disLine.segmentdirections,axis=1)
    disLine.clip(lambda c : segLens < 0.35 )  # remove segments too long.
    return disLine

# 2. Setup and map surfaces .........................................
rez = 6
cmu.hue_cmap('m','+m',name='myc')

surfaces,lines = [None]*2, [None]*2
surface = s3d.PlanarSurface(rez,color='grey').domain([-3,3],[-3,3])
surface.map_geom_from_op( coor_radius )
surfaces[0]=surface

conval = [ 2**i for i in range(-6,7)]
magval = [ 2*np.arctan(v)/np.pi  for v in conval]
line = surface.contourLines(*magval,color='k')
line.set_linewidth(1)
lines[0] = line

# note: higher rez due to surface discontinuity.
surface = s3d.PlanarSurface(rez+2,color='grey').domain([-3,3],[-3,3])
surface.map_geom_from_op( coor_theta )
disLine = discontinuity_contours(surface) #.. access before clipping
normals = surface.facenormals(v3d=False)
surface.clip(lambda c : isContinuous(c,normals))
surfaces[1]=surface

t_cbvals = [0.002, 0.25, 0.5, 0.75, 0.998]
t_axvals = [ v for v in t_cbvals ]
line = surface.contourLines(*t_axvals,color='r')
line.map_cmap_from_op( lambda c: c[2], 'myc' )
lines[1] = line

# 3. Construct figure, add surface, plot ............................

elev,azim = 20,150

r_labels = [ '0','1/8','1/4','1/2','1','2','4','8',r'$\infty$']
r_axvals = [0] + [ 2*np.arctan(2**i)/np.pi for i in range(-3,4)] + [1]
t_labels = [r'-$\pi$',r'-$\pi$/2','0',r'$\pi$/2',r'$\pi$']
t_axvals = [ v/4 for v in range(0,5)]
z_ticks = [r_axvals,t_axvals]
z_axlab = [r_labels,t_labels]
title = [ r'$\mathcal{R}$, magnitude', r'$\theta$, angle']

fig = plt.figure(figsize=plt.figaspect(0.5/1))
info = r" f(z) =  $\frac{(z^{2}-1)(z-2-i)^{2}}{z^{2}+2+2i}$  "
fig.text(0.5,1,info, ha='center', va='top', fontsize='x-large')
for i,surface in enumerate(surfaces) :
    ax = fig.add_subplot(121+i, projection='3d', aspect='equal')
    ax.view_init(elev,azim)
    #ax.view_init(89.9,-90.01)  # <-- 2D-view from top 
    ax.set_proj_type('ortho')
    ax.set_title('\n'+title[i],color='grey', fontsize='xx-large')
    ax.set(xlim=( -3,3 ), ylim=( -3,3 ), zlim=( 0,1), zticks=z_ticks[i],
                xlabel='Re(z)', ylabel='Im(z)' )
    ax.set_zticklabels(z_axlab[i])

    surface.set_surface_alpha(0.25)
    surface.shade(0.25,ax=ax,direction=[0,1,1])
    if i==1 : surface.hilite(0.7,direction=[0,1,1])
    ax.add_collection3d(surface)
    ax.add_collection3d(lines[i])

fig.tight_layout(pad=-2)

# =======================================================================
# Domain Color Map ======================================================

# 2. Setup and map surfaces .........................................
cmu.hue_cmap('m','+m',name='mycym')

surface = s3d.PlanarSurface(rez,cmap='mycym').domain([-3,3],[-3,3])
surface.map_color_from_op( domainColor, rgb=False )

line_0 = surfaces[0].contourLines(*magval)
line_0.map_cmap_from_op(lambda c: c[2], 'binary')
line_0.set_linewidth(.5)
line_1 = surfaces[1].contourLines(*t_axvals)
line_1 += disLine  # <-- add contours @ -pi and pi
line_1.map_cmap_from_op( lambda c: c[2], 'myc' )
line_1.set_linewidth(.5)

# 3. Construct figure, add surface, plot ............................

cbval_a = [-1,-.5,0,0.5,1]

fig = plt.figure(figsize=plt.figaspect(1))
fig.text(0.5,.92,info, ha='center', va='top', fontsize='x-large')

ax = plt.axes(projection='3d')
ax.set(xlim=( -3,3 ), ylim=( -3,3 ), zlim=( 0,1 ), 
            zticks=[], xlabel='Re(z)', ylabel='Im(z)' )
ax.view_init(89.9,-90.01)
ax.set_proj_type('ortho')
cbar = plt.colorbar(surface.cBar_ScalarMappable, ax=ax, ticks=cbval_a, shrink=0.6, pad=-.1 )
cbar.ax.set_yticklabels(t_labels)
cbar.set_label(r'$\theta$, angle', rotation=90, labelpad = 0)

sm = plt.cm.ScalarMappable(cmap='binary_r')
sm.set_array([])
cbar2 = fig.colorbar(sm, ax=ax, ticks=r_axvals,shrink=0.7, pad=-.1, orientation='horizontal' )
cbar2.ax.set_xticklabels(r_labels)
cbar2.set_label(r'$\mathcal{R}$, magnitude (reversed cmap for contours)')

ax.add_collection3d(surface)
ax.add_collection3d(line_0)
ax.add_collection3d(line_1)

fig.tight_layout(pad=0)
# =======================================================================
plt.show()