Inner and Outer Surface Coloring

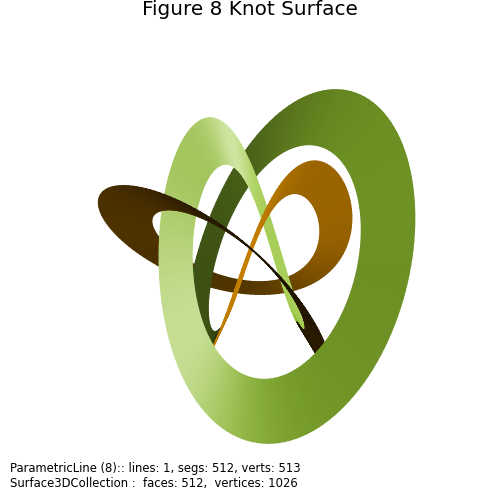
The functional form is taken from Figure-eight knot Surface is constructed using two parametric lines, differing only in size. The inner and outer surfaces are colored similarly to the method in the Inner/Outer Surface Colormap example. The colormap is shown below:

import numpy as np
from matplotlib import pyplot as plt
import s3dlib.surface as s3d
import s3dlib.cmap_utilities as cmu

#.. Figure 8 Knot Surface
# 1. Define function to examine .....................................

def fig_8_knot(t,isInner) :
    T = 2*np.pi*t
    x = (2 + np.cos(2*T))*np.cos(3*T)
    y = (2 + np.cos(2*T))*np.sin(3*T)
    z = 3*np.sin(4*T) 
    f = 0.8 if isInner else 1.2
    return f*x,f*y,f*z

inn_eight = lambda t : fig_8_knot(t,True)
out_eight = lambda t : fig_8_knot(t,False)

# 2. Setup and map line .............................................
rez=8
bcmap = cmu.binary_cmap('orange', 'yellowgreen', name='orng_yg' )

line_1 = s3d.ParametricLine(rez,inn_eight)
line_2 = s3d.ParametricLine(rez,out_eight)

surface = line_1.get_surface_to_line(line_2)

# 3. Construct figure, add surface, and plot ........................

fig = plt.figure(figsize=(5,5))
fig.text(0.02,0.02, '\n'+str(line_1)+'\n'+str(surface),
    ha='left', va='bottom', fontsize='smaller')
ax = plt.axes(projection='3d')
ax.set_title("Figure 8 Knot Surface",fontsize='x-large')
ax.set_axis_off()
ax.view_init(azim=-70)

s3d.auto_scale(ax,surface,uscale=.85)
surface.map_cmap_from_normals(direction=ax,cmap=bcmap)
ax.add_collection3d(surface.shade(ax=ax).hilite(ax=ax,direction=[1,-.4,1]))

fig.tight_layout(pad=0)
plt.show()