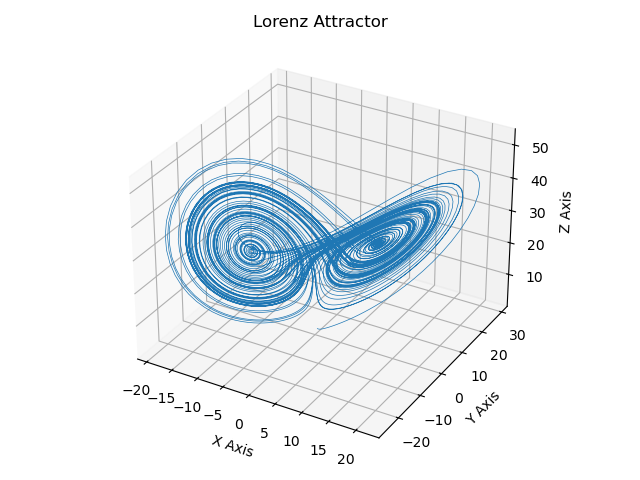
Lorenz Attractor

This is a comparison to the Lorenz Attractor Matplotlib example. Alternative coloring of this segmented line is given in the following examples:

• Segment Orientation Color.

• Sequential Line Color.

• Functional Line Color.

import numpy as np
import matplotlib.pyplot as plt
import s3dlib.surface as s3d

#.. Matplotlib Examples: Lorenz Attractor

# 1. Define function to examine .....................................

# +----------------------------------------------------------------------------
# |  The following code between the ========= comments was copied DIRECTLY from
# |  https://matplotlib.org/stable/gallery/mplot3d/lorenz_attractor.html#sphx-glr-gallery-mplot3d-lorenz-attractor-py
# |
# +----------------------------------------------------------------------------
# ===================================================== start of copy.

def lorenz(x, y, z, s=10, r=28, b=2.667):
    """
    Given:
       x, y, z: a point of interest in three dimensional space
       s, r, b: parameters defining the lorenz attractor
    Returns:
       x_dot, y_dot, z_dot: values of the lorenz attractor's partial
           derivatives at the point x, y, z
    """
    x_dot = s*(y - x)
    y_dot = r*x - y - x*z
    z_dot = x*y - b*z
    return x_dot, y_dot, z_dot

dt = 0.01
num_steps = 10000

# Need one more for the initial values
xs = np.empty(num_steps + 1)
ys = np.empty(num_steps + 1)
zs = np.empty(num_steps + 1)

# Set initial values
xs[0], ys[0], zs[0] = (0., 1., 1.05)

# Step through "time", calculating the partial derivatives at the current point
# and using them to estimate the next point
for i in range(num_steps):
    x_dot, y_dot, z_dot = lorenz(xs[i], ys[i], zs[i])
    xs[i + 1] = xs[i] + (x_dot * dt)
    ys[i + 1] = ys[i] + (y_dot * dt)
    zs[i + 1] = zs[i] + (z_dot * dt)

# ===================================================== end of copy.

lineCoor = np.array( [xs,ys,zs] ).T

# 2. Setup and map surfaces .........................................

line = s3d.SegmentLine( lineCoor, "Lorenz Attractor", lw=0.5 )

# 3. Construct figure, add surface, plot ............................

fig = plt.figure()
ax = plt.axes(projection='3d')
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title( line.name )
s3d.auto_scale(ax,line)

ax.add_collection3d(line)

fig.tight_layout()
plt.show()